| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 정보이론
- AirSim #RL #Drone
- vlm #clip #object detection
- 책 #오늘 밤
- planning #ste #논문 리뷰
- ROS2
- vlm 정리 #glip #object detection
- dino #grounding dino #vlm #object detection
- ROS1
- 세계에서 이 세상이 사라진다 해도
- Infotaxis
- ste
- 소울러닝 #책리뷰 #느낀점
- 탐색
- vision language model #transformer
- 개발 일기
- 경로 계획
- 코드 트리 #개발자 #언어 공부 #코딩 공부
- Unity
- 자율주행 #로봇공학과
- 로봇 #로봇공학과 #공대생 #대학생 #일상 #휴무 #교수
- path planning #mcts
- Today
- Total
퇴근할게요 교수님
Monte Carlo Tree Search [MCTS Path Planning] 본문
Monte Carlo Tree Search 알고리즘
알파고가 바둑으로 사람을 이긴 것으로 유명해지고 나서 지금까지, AI의 발전은 무궁무진하게 흘러갔다. MCTS는 알파고에서 사용된 알고리즘으로, 강화학습을 사용하는 사람들이나 불확실성에 관련한 연구를 진행하는 사람은 많이 들어봤을 주제이다.
MCTS는 시뮬레이션을 거쳐 가장 승률이 좋은 행동을 하는 알고리즘이다.
다만, 어떠한 행동을 할 지의 선택지를 정해 주어야 하며, 내가 정한 환경에서만 작동된다.

MCTS에 대해서 얘기 하기 전에 그 근본이 되는 MDP에 대해서 얘기해 보자.
MDP란 [Markov Decision Proccess]로, 시간 t에서의 상태는 t-1 에서의 상태에만 영향을 받는다는 정의를 기반으로, 현재 나의 상태에서 행동에 대해서 확률적으로 계산을 하는 것이다.
MCTS 또한, 현재 나의 상황에서 Tree 구조의 확률 계산을 통해서 어떠한 행동이 가장 높은 점수일 지를 계산하게 된다.
이제 MCTS의 단계에 대해서 알아보자.
Selection
현재 노드에서 어떤 노드로 가야할 지 결정하는 과정을 Selection이라고 한다. 이 때,
UCT[Upper Confidence Boundary of Tree] 라는 알고리즘을 사용하여 Exploration [탐험]과 Exploitation [이용]을 선택한다.
수식적으로 보도록 하자.

UCT의 공식은 다음과 같다.
$W_i$ : i 번 움직인 이후의 승리 횟수
$n_i$ : i번 움직인 이후의 시뮬레이션 횟수
$c$ : exploration parameter. c는 $sqrt(2)$를 기본으로 사용하지만, 실험을 통해서 조절한다.
$t$ : 시뮬레이션의 전체 횟수이다.
수식을 간단하게 설명해 보자.
한 번도 탐색되지 않은 노드면 $t = 0$ 임으로, bias 항이 무한대가 되어 반드시 한 번은 실행이 되게 될 것이다.
$W_i / n_i $는 임의의 child node $i$의 평균 보상을 의미한다. 이는 게임의 경우 승률에 해당하는 값이다.
오른쪽 항 $c*sqrt(ln(t) / n_i)$ 에서 $n_i$는 child node $i$의 방문 횟수, $t$는 그것의 parent node의 방문 횟수이다. 이 때, $n_i$가 분모에 있으므로 child node $i$의 방문 횟수가 작아지면 게임의 승률이 작아도 $c*sqrt(ln(t) / n_i)$의 값이 커지므로, 해당 node의 전체적이 값이 커져 선택될 확률이 높아진다.
이를 통해서 계산을 진행하고, MCTS의 단계를 그림으로 보면 다음과 같다.

Expansion
selection 이후 이동해서 멈출 노드의 확률을 생성한다.
한 노드의 방문 횟수가 일정 한계에 도달한다면, 대부분의 수행은 한 노드의 자식 노드의 확장을 진행하려고 한다.
Simulation
expansion 과정에서 만들어진 노드로부터 게임을 진행한다. 게임을 진행하며 random하게 선택을 하게 되며, 어떠한 데이터를 얻었는 지를 저장하며 다음 단계인 Backpropagation 으로 진행된다.
Backpropagation
트리의 뿌리로 다시 올라가는 과정이다.
자신이 가진 데이터를 바탕으로 어떠한 정보를 얻었는 지 Parent node를 업데이트 한다.
이 과정을 반복하며 뿌리를 내리고, 업데이트를 반복한다.
MCTS Path Planning
이제 MCTS의 개념에 대해서 어느정도 알았을 것이다. 그런데 이것으로 어떻게 Path Planning을 진행한다는 걸까?
Path Planning은 경로 계획으로 RRT, A*와 같은 알고리즘이 대표적이다. 이는 목적지 까지의 경로에 대해서 랜덤하게 생성하게 된다.
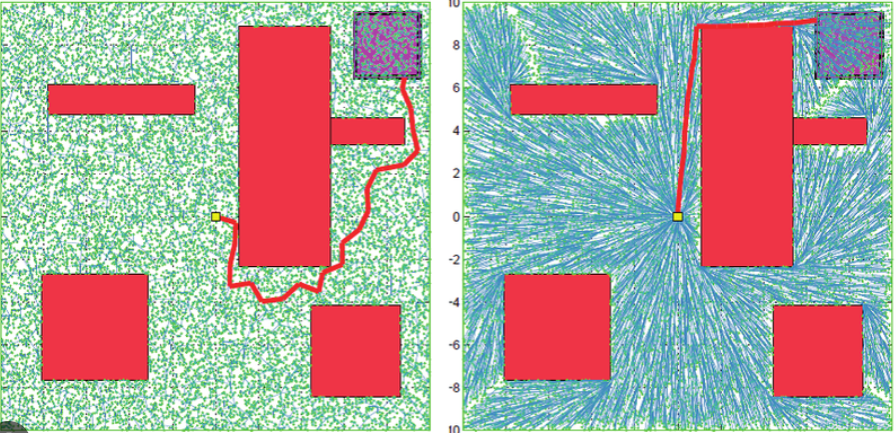
A*와 RRT는 둘다 Random 한 경로를 생성하게 된다. 즉, 최적의 경로에 대해서 구하는 것은 아니다.
이를 위해 MCTS 개념을 사용하게 된다. MCTS는 정해진 경로로 움직이며, 그 이후의 경로에 대해서 탐방하지 못한다는 단점이 있지만 특정 환경에서는 기존의 Path Planning보다 더 장점이 있을 수 있다.
차량에 대해서 생각해 보자. 우리의 차량에서는 이동할 수 있는 범위가 매우 작을 것이다. 이럴 때, 굳이 Random한 경로를 지녀 최적의 경로를 가지지 못한다는 것은 매우 비효율적으로 받아들여질 것이다.

MCTS는 정해진 경로에 대해서 뿌리를 내려 최적의 경로에 대해서 찾게 된다. 이러한 방식을 통해서 고정된 환경 내에서 랜덤성을 줄이고, 확률론적으로 최적의 경로에 대해서 생성할 수 있다는 장점이 있다.
이러한 특징에 대해서 알아보기 위해 Grid 한 환경에서 실험을 진행하였다.
다음과 같이 Tree Depth의 Max 값을 5로 지정하여 진행해 주었다.
최종적으로 MCTS를 가지고 Path Planning을 만들어 보았다. AI의 근간이 되는 알고리즘으로, 계산량이 복잡하고 고정된 Path로 이동해야 하는 문제가 존재하지만, 특정 환경에서 유용하게 사용할 수 있을 것이다.


